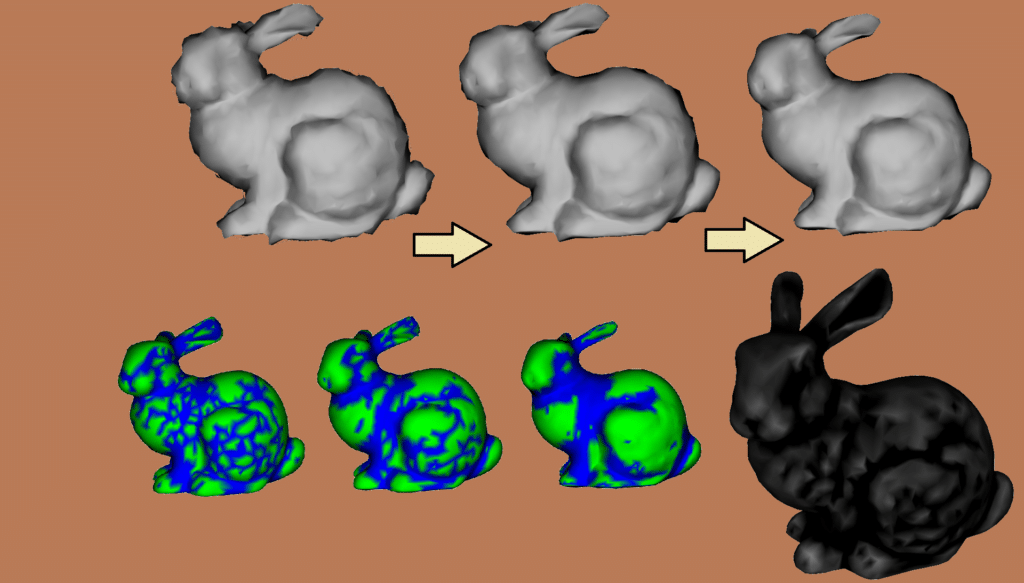
In this project, we tackled the ubiquitous problem of noise in scanned 3D models by implementing both explicit and implicit Laplacian-based denoising schemes. After acquiring a raw mesh—often riddled with high-frequency artifacts from imperfect scanning—we first computed key geometric features such as mean curvature, Gaussian curvature, and principal curvatures. These per-vertex quantities not only help us understand where noise is most pronounced but also guide the smoothing process so that sharp edges and fine details are preserved.
The core of the system applies Laplacian smoothing operators: an explicit filter performs iterative vertex updates based on the difference between a vertex and a weighted average of its neighbors, while the implicit variant solves a sparse linear system to diffuse noise more robustly in a single step. By blending these approaches, we achieved a balance between speed and stability—allowing interactive previews via OpenGL and a final high-quality pass using Eigen for fast matrix solves and LibANN for nearest-neighbor queries in feature-driven weighting.